روش خصوصيات (Method of Characteristics)

برای اهداف عملی ،علاوه برروش ساده شده ای که قبلا" اشاره شد،می توان ازروش ترسيمی مبتنی بر خصوصيات نيز استفاده کرد.

 خصوصيات ( Characteristics)

هرآشفتگی ياتغييری که درسطح جريان درنقطه ای ازكانالدرزمان روی دهد،منجربه انتشار امواج به سمت بالادست وپايين دست می شود.بنابراين ،چنانچه جريانی ،درنقطه  Q ،متلاطم شود،ناحيه هاشورزده درشکل 2-27 راکه بامنحنيهای +Cو-C نشان داده شده است تحت الشعاع خودقرارمی دهد.اين منحنيها ،مسيرانتشار امواج رانشان می دهد. اگر آشفتگی ايجاد شده درسطح جريان ،موج کم عمقی را با دامنه محدودايجادکند ، به خطوطی که مرزاين ناحيه هارانشان می دهد،منحنی خصوصيات گفته می شودومی توان آنها رادرصفحه  نشان داد. ازديدگاه رياضی ،آشفتگی سطح جريان ،به مفهوم ناپيوستگی مشتقات مرتبه اول ومرتبه های بالاتر متغيرهای وابسته وعوامل فيزيکی موجود درمعادلات حاکم به جريان است.بنابراين ،ناپيوستگی شيب سطح آب ياشيب سرعت باسرعتی برابرباسرعت انتشار درآب کم عمق،درطول منحنی خصوصيات پخش می شود:

برای مجاری منشوری (Prismatic Channels)باسطح مقطع وشيب کف ثابت،معادلات پيوستگی وديناميکی راچنين می توان نوشت:

که بامعرفی متغير جديدC به جای h ، به شکل خصوصيات تبديل می شود:

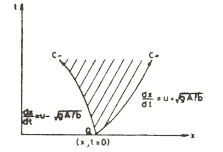
 محدوده اثرمنحنی خصوصيات

   با مشتقگيری از برحسب  t,X   وباتوجه به اينکهداريم:

و:

وباجايگذاری درروابط و، معادلات زير حاصل می شود:

دراينجا:

با جمع وسپس تفريق معادلات فوق می توان هردومعادله زيرراکه شکل خصوصياتی معادله جريان گفته می شود، به دست آورد:

اما و، نمايانگر سرعت جريان است.درحقيقت توابع Cوu درصفحه براساس معادله  مشتق گيری شده وارضاکننده معادلات ديفرانسيل هستند.مقادير داخل کروشه چيزی جزمشتق کل درامتداداين منحنيهانمی باشد:

بنابراين می توان نوشت:

*

بدين ترتيب ، برای هر ذره ای ازسيال که باسرعت درحال حرکت است معادله  قابل قبول بوده درطول منحنی خصوصيات به صورت زير تعريف می شود:

در حالی که معادله * برای منحنی خصوصيات  قابل قبول بوده به صورت زيرتعريف می شود:

با داشتن چهار معادله ديفرانسيلی فوق ، می توان چهار مشتق جزيی متغيرهای وابسته  رادر صفحه به دست آورده آنها راحل کرد. دركاناليی افقی که بتوان ازاصطکاک آن صرف نظر کرد، ؛ بنابراين طبق معادلات(2-51تا2-52) برای خصوصيات مثبت داريم:

برای خصوصيات منفی داريم :

مقادير  به مقادير ريمن(Reimann) مشهور است . بنابراين بااستفاده ازرابطه و مقادير،حل جريانهای تقريبا"افقی امکان پذير است .به چنين روشی،روش خصوصيات گفته می شود.بايد نوجه داشت که مقادير حل مقدماتی رابدست می دهد.بنابراين لازم است بدانيم چه رابطه ای متناسب بامقاديرريمن،برای كاناليی که شيب کف ومقاومت اصطکاکی آن باتنش برشینشان داده می شود ،وجوددارد.برای كاناليی باشيب بستر ملايم ، می توان نوشت: 

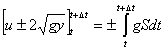
برای كاناليی بابستر کاملا" افقی، اگر تنش برشی باشدرابطه آن رانيزمی توان بدست آورد که درادامه آمده است.

اگر تنش برشی درجهت منفی عمل کند (مخالف  باشد) موج اوليه ،نه تنهابايدافزايشی دراندازه حرکت  ايجادکند؛ بلکه بايد افت دراندازه حرکت ناشی ازتنش برشی رانيز شامل شود.اين رابطه رابه صورت می توان نوشت.دراينجاچگالی سيال است. بنابراين داريم:

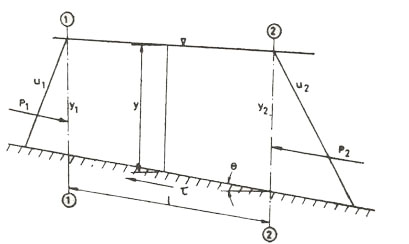
 ضرايب اصلاحي ناشي ازتنش برشي

باانتگرالگيری (نسبت به  ) می توان نوشت(شکل فوق):

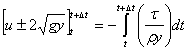
دراينجا:

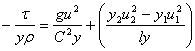
مقادير داخل پرانتز درروابط و 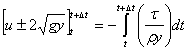به عنوان اجزای اصلاحی درصفحه که صفحه هودوگراف ناميده می شود- کاربرددارد.

همچمنين نگاه كنيد به...

• روشهاي هيدروليكي رونديابي سيلاب

• روش ماسكينگام

•  امواج سيلاب دررودخانه هايامجاري طبيعي