فصل نهم: آب زير زميني

روش ژاكوب

ژاكوب با اين استنتاج كه در معادله تيس اگر u<0.01 باشد ( و يا         ) مقدار عبارت  

چندان زياد نسبت معادله تيس را به صورت زير در نظر گرفت

 

اگر از يك منحني در سمت راست معادله فاكتور گرفته شود و به جاي عدد -0.5772 عبارت ln 1.78 گذاشته شود خواهيم داشت :

 

 

در پايه لگاريتم 10 داريم

 

در معادله فوق r  فاصله چاه مشاهده‌اي از چاه پمپاژ (در صورتي كه يكي باشند شعاع چاه)، Q دبي ثابت پمپاژ، S ضريب ذخيره، T ضريب انتقال و H-h مقدار افت و t زمان از شروع پمپاژ است. براي آنكه منحني را از رابطه بالا حذف كنيم جاي صورت مخرج عبارت جلو لگاريتم را جابجا مي‌كنيم:

 

فرمول ژاكوب را مي‌توان به صورت زير هم نوشت:

 

 

 


مي‌توان فرمول فوق را به عنوان خطي با ضريب زاويه           در نظر گرفت. در اين روش ابتدا در يك دستگاه نيمه لگاريتمي تغييرات افت (H-h) را بر حسب لگاريتم زمان ترسيم نموده و سپس خطي از بين نقاط داده‌ها عبور داده مي‌شود، به ازاء يك دستگاه لگاريتمي زمان (مثلاً 1 تا 10 يا 10 تا 100) ضريب زاويه C برابر خواهد بود با Δh چون

 

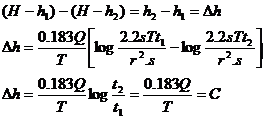
بنابراين با داشتن Δh مي‌توان T را محاسبه نمود :

از طرفي در محل برخورد خط يا منحني با محور زمان (H-h) يا مقدار افت صفر است. زمان بدست آمده به ازاء افت صفر را t0 مي‌ناميم:

 

 


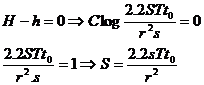
اين روش عليرغم سادگي انعطاف قابل قبولي در حالتهاي مختلف دارد. از روش فوق مي‌توان زماني كه چاه مشاهده‌اي در نزديكي چاه پمپاژ است و دبي با مقدار ثابتي برداشت مي‌شود، در نظر گرفتن شعاع چاه به جاي فاصله از چاه (r) استفاده نمود.

 اگر اندازه‌گيري در يك پيزومتر و چند آزمايش پمپاژ با دبي ثابت انجام شود نيز مي‌توان معادله ژاكوب را به صورت زير نوشت تا افت مخصوص را بدست دهد:

 

كه معادله خطي با ضريب زاويه C مي‌باشد. اگر در يك سيكل لگاريتمي ΔDs (اختلاف افت مخصوص) محاسبه شود از فرمول زير مي توان ضريب انتقال را محاسبه نمود :

 

 ضريب ذخيره نير به همان روش قبلي از طريق بدست آوردن محل تلاقي منحني با محور زمان (t0) قابل محاسبه است :

 

چناچه پمپاژ با دبي ثابت در يك چاه اصلي صورت گيرد و اندازه‌گيري پيزومتري در چند پيزومتر صورت گيرد مي‌توان با تشكيل منحني است و        ضرايب هيدروديناميكي آبخوان را محاسبه نمود. فرمول ژاكوب را مي‌توان بصورت زير نوشت.

 

كه ضريب زاويه همانند روشهاي قبلي برابر است با :

 

بنابراين براي يك سيكل لگاريتمي مقدار T برابر است يا :

 

 

چناچه خط را ادامه داده تا محور زمان را قطع كند ( نقطه      ) خواهيم داشت :

 

 

 توجه:
 © به موجب قانون حقوق مولفين، كليه  حقوق مادي و معنوي اين اثر الکترونيکي براي نويسنده  (خدايار عبداللهي) محفوظ است.  هرگونه كپي برداري، نقل قول، تبديل به قالب هاي ديگرو... بدون ذكر منبع ممنوع است. در اختيار گذاشتن  رايگان اين اثر صرفاً  براي استفاده هاي علمي بوده  و توزيع تجاري آن بدون مجوز صاحب اثر غير قانوني مي باشد.                                             

| آغازفصل| فهرست|بازگشت | صفحه اصلي